

Next: 6.1 グラフの記述
Up: ソフトウェア第三 講義資料 行列,リスト操作,グラフ,探索表現
Previous: 5.4 状態表現の一般化
6 グラフ
グラフ(graph)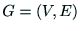 は,頂点(vertex)が空でない有限集合
は,頂点(vertex)が空でない有限集合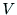 と辺(edge)の
集合
と辺(edge)の
集合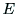 からなるものととらえることができる.
辺が頂点の順序対
からなるものととらえることができる.
辺が頂点の順序対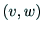 で与えられる場合は,そのグラフは
有向(directed)グラフと呼ばれる.
で与えられる場合は,そのグラフは
有向(directed)グラフと呼ばれる.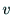 を
を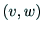 の始点(head),
の始点(head),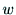 を終点(tail)と呼ぶ.
辺が互いに異なる頂点である非順序対
を終点(tail)と呼ぶ.
辺が互いに異なる頂点である非順序対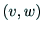 のグラ
フは無向(undirected)グラフと呼ばれる.
辺が互いに異なるということから
のグラ
フは無向(undirected)グラフと呼ばれる.
辺が互いに異なるということから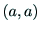 は有向グラフの辺であるが,無向グラフ
の辺ではない.
グラフ
は有向グラフの辺であるが,無向グラフ
の辺ではない.
グラフ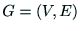 において
において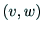 が
が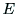 に含まれるならば,頂点
に含まれるならば,頂点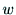 は頂点
は頂点
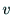 に隣接(adjacent)するといいます.頂点
に隣接(adjacent)するといいます.頂点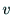 に隣接する頂点の個数を
に隣接する頂点の個数を
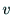 の次数(degree)という.
の次数(degree)という.
- 道(path)
道(パス)とは
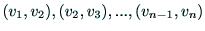 という形をした
辺の列のことである.この場合,
という形をした
辺の列のことである.この場合,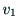 から
から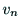 までの道といい,その長
さが
までの道といい,その長
さが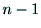 であるという.1個の頂点は長さ0の道である.単純(simple)
な道とは,その辺と頂点がすべて異なる道のことである.閉路(cycle)
とは,ある頂点から始まりその頂点で終るような長さ1以上の単純な道のこと
である.無向グラフでは閉路の長さは3以上である.
グラフのどの2点
であるという.1個の頂点は長さ0の道である.単純(simple)
な道とは,その辺と頂点がすべて異なる道のことである.閉路(cycle)
とは,ある頂点から始まりその頂点で終るような長さ1以上の単純な道のこと
である.無向グラフでは閉路の長さは3以上である.
グラフのどの2点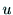 ,
,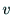 に対しても
に対しても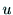 から
から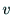 へパスがあるとき,そのグラ
フは連結(connected)であると呼ばれる.
へパスがあるとき,そのグラ
フは連結(connected)であると呼ばれる.
- 隣接行列(adjacency matrix)
グラフの表現方法の一つ.グラフ
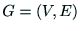 の隣接行列
の隣接行列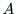 は,集合
は,集合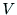 の要素
の個数
の要素
の個数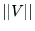 次の正方行列であり,要素が0または1のものである.
次の正方行列であり,要素が0または1のものである.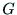 に辺
に辺
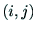 が存在する時のみ,
が存在する時のみ,![$A[i,j]=1$](img52.png) をもつ.辺が存在するかどうかを頻繁
に判定する場合には有効だが,記憶場所が
をもつ.辺が存在するかどうかを頻繁
に判定する場合には有効だが,記憶場所が 必要となり隣接行列の
初期値を与えるだけでも時間がかかってしまう.行または列をビットベクトル
で表現する方法もある.
必要となり隣接行列の
初期値を与えるだけでも時間がかかってしまう.行または列をビットベクトル
で表現する方法もある.
- 隣接点リスト(adjacency list)
頂点
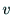 の隣接点リストとは,
の隣接点リストとは,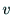 に隣接するすべての頂点
に隣接するすべての頂点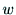 のリストのことである.
記憶領域は
のリストのことである.
記憶領域は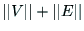 に比例する.
に比例する.
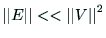 の時によく使われる.
の時によく使われる.
generated through LaTeX2HTML. M.Inaba 平成18年5月7日