

Next: 2.2 余因子展開
Up: 2 余因子,行列式,逆行列
Previous: 2 余因子,行列式,逆行列
n次元行列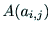 の(i,j)余因子(cofactor)
の(i,j)余因子(cofactor)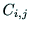 とは,
行列Aのi行,j列を除いた(n-1)次元の
小行列
とは,
行列Aのi行,j列を除いた(n-1)次元の
小行列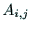 の行列式
の行列式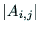 に符号として
に符号として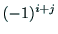 をつけたものである.
をつけたものである.
m-cofactorは,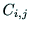 を求める.これを求めるには,
を求める.これを求めるには,
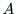 の小行列
の小行列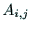 を求めるminor-mをまず定義し,
行列式を求めるm-detを用いて定義することとする.
を求めるminor-mをまず定義し,
行列式を求めるm-detを用いて定義することとする.
(defun m-cofactor (m i j)
(if (oddp (+ i j))
(- (m-det (minor-m m i j)))
(m-det (minor-m m i j)))
)
ここで,oddpは,引数が奇数であればtを返す.
minor-mは,行列Aのi行の行ベクトルを除いた行列を返す
drop-rowをまず定義して次のように定義することとする.
(defun minor-m (m i j)
(transpose (drop-row (transpose (drop-row m i)) j))
)
(defun drop-row (m i)
(let ((ret nil))
(dotimes (j (length m))
(if (not (= i j))
(setq ret (cons (car m) ret)))
(setq m (cdr m)))
(reverse ret)))
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![$\displaystyle A_{i,j} =\left[
\begin{array}{cccccc}
a_{1,1} & \cdots & a_{1,j-1...
...n,1} & \cdots & a_{n,j-1} & a_{n,j+1} & \cdots & a_{n,n} \\
\end{array}\right]$](img6.png)
![$\displaystyle A_{i,j} =\left[
\begin{array}{cccccc}
a_{1,1} & \cdots & a_{1,j-1...
...n,1} & \cdots & a_{n,j-1} & a_{n,j+1} & \cdots & a_{n,n} \\
\end{array}\right]$](img6.png)