2.4 逆行列

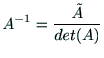
Next: 3 リスト構造の変更 Up: 2 余因子，行列式，逆行列 Previous: 2.3 余因子行列

2.4 逆行列

行列の余因子行列から行列の逆行列を求めることができる． n次正方行列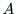

の行列式を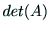

をし，n次単位行列を

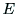とすると

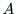とその余因子行列 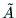$\tilde{A}$ に対して，

$\displaystyle A\tilde{A} = \tilde{A}A = det(A)E$

という関係が成り立つ．よって，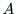

の逆行列は，

$\displaystyle A^{-1} = \frac{\tilde{A}}{det(A)}$

として求められる．よって，逆行列を求めるm-inverseを m-det, adjoint-mを使って定義すると次のように定義できる．

(defun m-inverse (m)
  (scale-m (/ 1.0 (m-det m)) (adjoint-m m)))

ここで，scale-mは，行列の各要素を定数倍するというものであり，次のように定義できる．

(defun scale-v (s v)
  (mapcar #'(lambda (x) (* s x)) v))

(defun scale-m (s m)
  (mapcar #'(lambda (x) (scale-v s x)) m))

逆行列を求めてみると，

(setq c '((1 2) (3 4)))
((1 2) (3 4))
(m-det c)
-2.0
(m-inverse c)
((-2.0 1.0) (1.5 -0.5))
(m* c (m-inverse c))
((1.0 0.0) (0.0 1.0))
(m* (m-inverse c) c)
((1.0 0.0) (0.0 1.0))

(setq a '((10 20) (4 30)))
((10 20) (4 30))
a
((10 20)
 (4 30))
(m-det a)
220.0
(m-inverse a)
((0.13636363636363635 -0.09090909090909091)
 (-0.01818181818181818 0.045454545454545456))
(m* (m-inverse a) a)
((0.9999999999999999 -4.440892098500626e-016)
 (0.0 1.0))

というようになる． 2x2行列だけでなく，3x3行列でも，

b
((1 2 3) (4 5 9) (9 8 7))
(m-det b)
30.0
(m-inverse b)
((-1.2333333333333334 0.3333333333333333 0.1)
 (1.7666666666666666 -0.6666666666666666 0.1)
 (-0.43333333333333335 0.3333333333333333 -0.1))

(m* b (m-inverse b))
((0.9999999999999998 0.0 0.0)
 (-1.7763568394002505e-015 1.0000000000000002 0.0)
 (-1.7763568394002505e-015 0.0 1.0))

(m* (m-inverse b) b)
((0.9999999999999999 -2.220446049250313e-016
          -1.1102230246251565e-016)
 (1.1102230246251565e-016 1.0000000000000002
          -1.1102230246251565e-016)
 (-1.1102230246251565e-016 -2.220446049250313e-016
           0.9999999999999999))

と同じ手続きを用いることができる．

generated through LaTeX2HTML. M.Inaba 平成18年5月7日