

Next: 2.4 逆行列
Up: 2 余因子,行列式,逆行列
Previous: 2.2 余因子展開
n次正方行列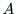 の余因子行列
の余因子行列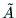 は,その(i,j)要素が
は,その(i,j)要素が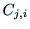 と
なるようにしたものである.
と
なるようにしたものである.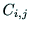 を要素にする行列を
を要素にする行列を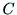 とすると,
とすると,
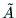 は
は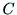 の転置行列となる.
の転置行列となる.
まず,余因子を要素とする行列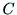 を求めるcofactor-mを
次のように定義する.
を求めるcofactor-mを
次のように定義する.
(defun cofactor-m (m)
(let ((mat (copy-tree m)))
(dotimes (i (m-row-size mat))
(dotimes (j (m-col-size mat))
(m-replace! mat i j (m-cofactor m i j))
))
mat))
ここで,copy-treeは,引数で与えられたリストのコピーを
作ることを行う組込み関数である.
(setq b '((1 2 3) (4 5 9) (9 8 7)))
((1 2 3) (4 5 9) (9 8 7))
(copy-tree b)
((1 2 3) (4 5 9) (9 8 7))
b
((1 2 3) (4 5 9) (9 8 7))
(copy-tree '(1 2 (3) ((5))))
(1 2 (3) ((5)))
というようになり,
(defun my-copy-tree (x)
(cond
((atom x) x)
(t (cons (my-copy-tree (car x))
(my-copy-tree (cdr x))))))
my-copy-tree
(my-copy-tree b)
((1 2 3) (4 5 9) (9 8 7))
b
((1 2 3) (4 5 9) (9 8 7))
という具合に定義できるものである.
m-row-size,m-col-sizeは,行列の行,列の大きさを返す.
(defun m-row-size (m) (length (car m)))
(defun m-col-size (m) (length m))
(m-replace! m i j v)は,行列m の(i,j)要素をvに
する関数である.
(defun m-replace! (mat i j value)
(v-replace! (elt mat i) j value)
mat)
(defun v-replace! (vec i value)
(let ((v vec))
(dotimes (j (length v))
(if (= i j) (rplaca v value))
(setq v (cdr v)))
vec))
ここで,rplacaは,元のリストデータのcar部の要素を
付け替えてしまう関数である.このような
元のリストデータを変更してしまう処理は破壊的な操作関数(destructive function)と
呼ばれる.
通常のリスト処理ではcons手続きによってデータを作って
ゆくことで,元のデータの構造を変更することは無い.
それは,元のデータへのポインタが利用されているだけであって
そのポインタからたどってゆけるデータの内部のポインタを
付け替えるということを行わないということである.
新しいリスト構造を作る際には,元のリストの
コピーを作りながら作るという形になっていた.
たとえば,(append x y)の場合には,xの構造をコピーした
ものへyをつなぐことを行う.
xがさしているデータには影響は与えない.
しかし,xのデータが大きい場合にコピーを作ることが
無駄で,xからたどれるデータ自体を変更してもよい場合には,
xからたどるデータの最後をnilへつなぐのではなく,
yにつなぐことによってappendされたデータをxの
データとすることもできる.このような処理を行う
手続きとしてnconcというものが組み込み関数として
用意されている.
行列データのような場合には,要素数の多いデータに対して
その一部のみの要素を変更したいという操作が通常の処理と
して行われる.行列をリストで表現した場合に,
変更したい部分だけ変えて残りの行列全体をコピーして
作るということを行うのは無駄が多くなる.
そこで通常は,配列データなどはリストで表現せずに
その要素の場所を直接指定して,その要素を置き換えて
ゆくことを行い,データのコピーは作らない形にする.
ここで上げた,m-replace!はリストデータで表現された
行列の要素の場所を指定して,その値を書き換えるという
ものである.
(setq a '((1 2) (4 3)))
((1 2) (4 3))
a
((1 2) (4 3))
(m-replace! a 0 0 10)
((10 2) (4 3))
a
((10 2) (4 3))
(m-replace! a 1 1 30)
((10 2) (4 30))
(m-replace! a 0 1 20)
((10 20) (4 30))
(m-det a)
220.0
(m-cofactor a 0 0)
30
(m-cofactor a 0 1)
-4
(m-cofactor a 1 0)
-20
(m-cofactor a 1 1)
10
(cofactor-m a)
((30 -4) (-20 10))
余因子行列は,cofactor-mで作られる行列の転置行列である.
よって,余因子行列を求める関数をadjoint-mとすると,
次のように定義できる.
(defun adjoint-m (m)
(transpose (cofactor-m m))
)
a
((10 20) (4 30))
(cofactor-m a)
((30 -4) (-20 10))
(adjoint-m a)
((30 -20) (-4 10))
b
((1 2 3) (4 5 9) (9 8 7))
(cofactor-m b)
((-37.0 53.0 -13.0) (10.0 -20.0 10.0) (3.0 3.0 -3.0))
(adjoint-m b)
((-37.0 10.0 3.0) (53.0 -20.0 3.0) (-13.0 10.0 -3.0))
(m-det b)
30.0
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![$\displaystyle \left[
\begin{array}{ccccc}
C_{1,1} & C_{2,1} & C_{3,1} & \cdots ...
...vdots \\
C_{1,n} & C_{2,n} & C_{3,n} & \cdots & C_{n,n} \\
\end{array}\right]$](img25.png)
![$\displaystyle \left[
\begin{array}{ccccc}
C_{1,1} & C_{2,1} & C_{3,1} & \cdots ...
...vdots \\
C_{1,n} & C_{2,n} & C_{3,n} & \cdots & C_{n,n} \\
\end{array}\right]$](img25.png)