

Next: 1.2 座標系の設定
Up: 1 ロボットアーム
Previous: 1 ロボットアーム
ロボットアームの空間リンクを解析するために図5のように,
座標系を設定すれば,座標変化を同一形式で扱うことができる.座標系
 がリンク
がリンク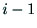 に固
定されているものとする.
リンク
に固
定されているものとする.
リンク に座標系
に座標系
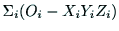 を固定する場合に,リ
ンク
を固定する場合に,リ
ンク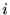 とリンク
とリンク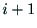 の連結部のジョイント
の連結部のジョイント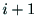 の軸を
の軸を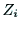 軸として選ぶ.
軸として選ぶ.
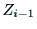 軸と
軸と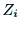 軸の共通垂線を考え,この共通垂線と
軸の共通垂線を考え,この共通垂線と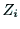 軸の交点を
軸の交点を
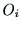 ,
,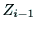 軸との交点を
軸との交点を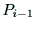 とする.
とする.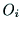 を
を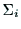 の原点と
し,
の原点と
し,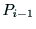 から
から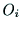 に向かう直線上に
に向かう直線上に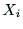 を定める.
を定める.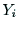 軸は右手系の
座標系を構成するように定める.このようにして決定された座標系
軸は右手系の
座標系を構成するように定める.このようにして決定された座標系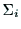 をリンク
をリンク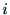 に固定されたものと考える.
に固定されたものと考える.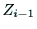 軸と
軸と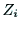 軸のなす角を
軸のなす角を
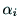 ,
,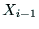 軸と
軸と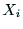 軸のなす角を
軸のなす角を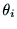 ,
,
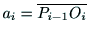 ,
,
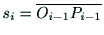 と
すれば,
と
すれば,
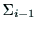 と
と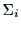 の間の座標変換は,4つのパラメタ
の間の座標変換は,4つのパラメタ
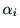 ,
,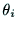 ,
,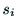 ,
,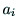 を用いて次式のように表される.
これら4つのパラメタによる記法はデナビット-ハーテンバーグ記法(D-H記法)と呼
ばれる.
を用いて次式のように表される.
これら4つのパラメタによる記法はデナビット-ハーテンバーグ記法(D-H記法)と呼
ばれる.
![$\displaystyle \left[
\begin{array}{c}
X_{i-1} \\
Y_{i-1} \\
Z_{i-1} \\
1
\end{array}\right]$](img47.png) |
|
|
(1) |
![$\displaystyle =\left[
\begin{array}{cccc}
c\theta_i & -\cos\alpha{_i}s\theta_i ...
...
\left[
\begin{array}{c}
X_i \\
Y_i \\
Z_i \\
1
\end{array}\right]
\nonumber$](img48.png) |
|
|
|
この4次の座標変換行列を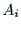 とする.ジョイント
とする.ジョイント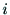 が回転の自由度の
とき,
が回転の自由度の
とき,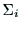 はリンク
はリンク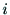 とともに,リンク
とともに,リンク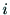 の軸すなわち
の軸すなわち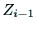 軸
のまわりに回転する.このとき,
軸
のまわりに回転する.このとき,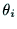 がジョイント
がジョイント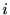 の回転角を表す
変数となる.パラメタ
の回転角を表す
変数となる.パラメタ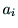 ,
,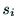 ,
,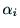 はリンク
はリンク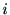 の形状に
よって決まる定数であり,
の形状に
よって決まる定数であり,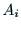 は
は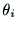 の関数となる.ジョイント
の関数となる.ジョイント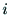 が
伸縮の自由度の時には,
が
伸縮の自由度の時には,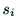 が変数であり,
が変数であり,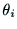 ,
,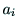 ,
,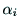 が定数である.
が定数である.
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![\includegraphics[width=8cm]{/home/inaba/text/iwanami/inaba/chap4/link-Aparam-org.eps}](img12.png)