

Next: 5.3 僇儊儔僉儍儕僽儗乕僔儑儞
Up: 5 帇妎僔僗僥儉
Previous: 5.1 僇儊儔儌僨儖
俁師尦嬻娫拞偺僇儊儔嵗昗宯偺揰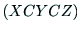 偐傜僇儊儔偺嶣憸柺偺嵗昗(
偐傜僇儊儔偺嶣憸柺偺嵗昗(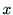 丆
丆
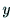 )偑寛傑傝丆寁嶼婡偱張棟傪峴偆僨僕僞儖夋憸嵗昗(
)偑寛傑傝丆寁嶼婡偱張棟傪峴偆僨僕僞儖夋憸嵗昗(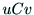 )傑偱偺嵗昗曄姺
偵昁梫側僷儔儊僞傪媮傔傞偙偲傪僇儊儔僉儍儕僽儗乕僔儑儞偲偄偆丏
嵗昗(
)傑偱偺嵗昗曄姺
偵昁梫側僷儔儊僞傪媮傔傞偙偲傪僇儊儔僉儍儕僽儗乕僔儑儞偲偄偆丏
嵗昗(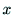 丆
丆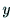 )偐傜(
)偐傜(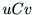 ) 傊偺曄姺偼丆夋憸拞怱偺嵗昗偺
僨僕僞儖夋憸嵗昗傪
) 傊偺曄姺偼丆夋憸拞怱偺嵗昗偺
僨僕僞儖夋憸嵗昗傪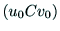 偲偟丆u,v幉偺側偡妏傪
偲偟丆u,v幉偺側偡妏傪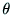 偲偟偰丆
u,v幉偺扨埵挿傪x,y幉傪婎弨偵偦傟偧傟
偲偟偰丆
u,v幉偺扨埵挿傪x,y幉傪婎弨偵偦傟偧傟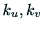 偲偡傞偲丆
偲偡傞偲丆
![$\displaystyle \left[
\begin{array}{c}
u \\
v \\
1 \\
\end{array}\right]
= H
\left[
\begin{array}{c}
x \\
y \\
1 \\
\end{array}\right]$](img304.png) |
|
|
(36) |
![$\displaystyle = \left[
\begin{array}{ccc}
k_u & -k_u\cot{\theta} & u_0 \\
0 & ...
...\end{array}\right]
\left[
\begin{array}{c}
x \\
y \\
1 \\
\end{array}\right]$](img305.png) |
|
|
(37) |
偲側傞丏
projection傛傝丆
![$\displaystyle \lambda\left[
\begin{array}{c}
u \\
v \\
1 \\
\end{array}\right]
= HP_f
\left[
\begin{array}{c}
X \\
Y \\
Z \\
1 \\
\end{array}\right]$](img306.png) |
|
|
(38) |
![$\displaystyle = \left[
\begin{array}{cccc}
fk_u & -fk_u\cot{\theta} & u_0 & 0 \...
...rray}\right]
\left[
\begin{array}{c}
X \\
Y \\
Z \\
1 \\
\end{array}\right]$](img307.png) |
|
|
(39) |
徟揰嫍棧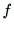 偺曄壔偲夋慺偺僒僀僘
偺曄壔偲夋慺偺僒僀僘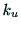 丆
丆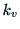 偺斾棪偺曄壔傪嬫暿偱偒側偄
偨傔偵偙傟傜傪堦懱壔偟偨僷儔儊僞傪峫偊丆
偺斾棪偺曄壔傪嬫暿偱偒側偄
偨傔偵偙傟傜傪堦懱壔偟偨僷儔儊僞傪峫偊丆
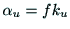 丆
丆
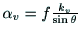 丆
丆
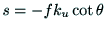 偲偟偰丆
偲偟偰丆
![$\displaystyle A = \left[
\begin{array}{ccc}
\alpha_u & s & u_0 \\
0 & \alpha_v & v_0 \\
0 & 0 & 1\\
\end{array}\right]$](img314.png) |
|
|
(40) |
傪峫偊傞丏
A偼咲酓錯崆攴毺camera intrinsic matrix)偲屇偽傟丆
俆偮偺僷儔儊僞
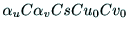 偼
僇儊儔屌桳偺傕偺偱偁傝丆崆耆橿intrinsic parameters)偲
屇偽傟傞丏
偼
僇儊儔屌桳偺傕偺偱偁傝丆崆耆橿intrinsic parameters)偲
屇偽傟傞丏
generated through LaTeX2HTML. M.Inaba 暯惉18擭5寧7擔
![\includegraphics[width=6cm]{/home/inaba/text/iwanami/inaba/chap4/gijiperspective.eps}](img291.png)