

Next: 5.4 エピポーラ幾何
Up: 5 視覚システム
Previous: 5.2 近似変換
画像列からカメラの内部変数を求めることをカメラキャリブレーションという.
カメラキャリブレーションは,三次元空間におけるある基準座標系中の
複数の点の座標とその点の投影点から射影を定める射影行列を求め,
射影行列から内部変数と外部変数を求めるという2段階の手順で考える.
射影行列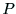 は,3x4の行列で,12個の要素がある.
は,3x4の行列で,12個の要素がある.
![$\displaystyle P = \left[
\begin{array}{cccc}
p_{11} & p_{12} & p_{13} & p_{14} ...
... & p_{23} & p_{24} \\
p_{31} & p_{32} & p_{33} & p_{34} \\
\end{array}\right]$](img317.png) |
|
|
(41) |
![$\displaystyle \lambda\left[
\begin{array}{c}
u \\
v \\
1 \\
\end{array}\right]
= P
\left[
\begin{array}{c}
X \\
Y \\
Z \\
1 \\
\end{array}\right]$](img318.png) |
|
|
(42) |
カメラの内部変数は5,
カメラの外部変数は回転3,並進3で合計11個である.Pには定数倍の
不定性があるため,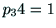 と仮定して残りの11個の要素を求める.
三次元の点
と仮定して残りの11個の要素を求める.
三次元の点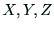 とその投影点
とその投影点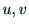 が既知であれば,
が既知であれば,
が成り立つ.射影行列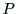 の11個の要素ベクトル
の11個の要素ベクトル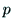 を得るために,
を得るために,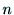 個の
個の
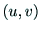 と(
と(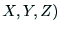 が得られれば,行列Bを縦にn個並べて
が得られれば,行列Bを縦にn個並べて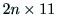 の
行列を作り,
の
行列を作り,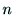 が6以上であれば
が6以上であれば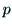 を求めることができる.
このように求めた射影行列
を求めることができる.
このように求めた射影行列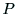 は,内部行列と三次元空間での回転と並進を組
み合わせたものであるため,
は,内部行列と三次元空間での回転と並進を組
み合わせたものであるため,
![$\displaystyle P = A
\left[
\begin{array}{cccc}
& & & \\
& {\rm R} & & {\rm t} \\
& & & \\
\end{array}\right]$](img332.png) |
|
|
(43) |
![$\displaystyle =
A\left[
\begin{array}{cccc}
r_{11} & r_{12} & r_{13} & t_1 \\
...
...r_{22} & r_{23} & t_2 \\
r_{31} & r_{32} & r_{33} & t_3 \\
\end{array}\right]$](img333.png) |
|
|
(44) |
となる.
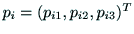 ,
,
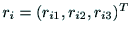 と置けば,
と置けば,
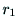 ,
,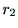 ,
,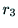 が
互いに直交することに注意しながら,
が
互いに直交することに注意しながら,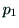 と
と
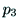 の外積,
の外積,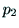 と
と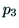 の
外積を計算し,それらの大きさをとる.
の
外積を計算し,それらの大きさをとる.
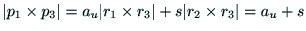 |
|
|
(48) |
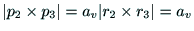 |
|
|
(49) |
であることがわかる.次に,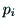 の互いの内積を
とって,
の互いの内積を
とって,
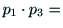 |
|
|
(50) |
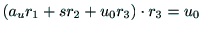 |
|
|
(51) |
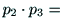 |
|
|
(52) |
 |
|
|
(53) |
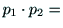 |
|
|
(54) |
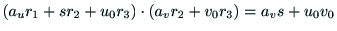 |
|
|
(55) |
となる.これらの関係式より,
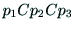 が得られれば,
内部パラメタ
が得られれば,
内部パラメタ
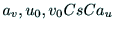 を求めることができる.
を求めることができる.


Next: 5.4 エピポーラ幾何
Up: 5 視覚システム
Previous: 5.2 近似変換
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![$\displaystyle P = \left[
\begin{array}{cccc}
p_{11} & p_{12} & p_{13} & p_{14} ...
... & p_{23} & p_{24} \\
p_{31} & p_{32} & p_{33} & p_{34} \\
\end{array}\right]$](img317.png)
![$\displaystyle \lambda\left[
\begin{array}{c}
u \\
v \\
1 \\
\end{array}\right]
= P
\left[
\begin{array}{c}
X \\
Y \\
Z \\
1 \\
\end{array}\right]$](img318.png)