

Next: 5.5 両眼立体視のカメラキャリブレーション
Up: 5 視覚システム
Previous: 5.3 カメラキャリブレーション
画像間の幾何関係を┘團檗璽藉𣝣燭箸いΑタA HREF="node25.html#epipolar-geometry">16のよ
うに,2つのカメラとそれぞれの撮像面に対して,それぞれのカメラ中心を他
方の撮像面に投影した点を┘團檗璽epipole)と呼び,撮像面上で注
視対象点の投影点とエピポールを通る直線を┘團檗璽蘋epipolar
line)と呼ぶ.2つのカメラ中心と注視対象点を通る面を┘團檗璽虧
(epipolar plane)と呼ぶ.両眼立体視において,注視対象を決めた時に,注視
対象の対応点を探す処理は,他方の投影面上のエピポーラ線上を1次元探索
することになる.
注目する点の2つのカメラ座標系での座標を
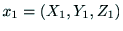 ,
,
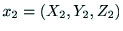 とし,2つの投影面への投影点を
とし,2つの投影面への投影点を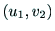 ,
,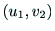 とすると,
2つのカメラ中心からの対象点までのベクトル
とすると,
2つのカメラ中心からの対象点までのベクトル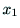 と
と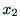 が
エピポーラ面上にあることから,それらの外積は0になる.
2つのカメラ座標系間の回転と並進を
が
エピポーラ面上にあることから,それらの外積は0になる.
2つのカメラ座標系間の回転と並進を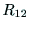 ,
, で表すと,
で表すと,
 |
|
|
(56) |
一般に,ベクトル との外積は,
3x3の歪対称行列
との外積は,
3x3の歪対称行列![$[{x ¥times}]$](img368.png)
![$¥displaystyle [{x ¥times}] =
¥left[
¥begin{array}{ccc}
0 & -x_3 & x_2 ¥¥
x_3 & 0 & -x_1 ¥¥
-x_2 & x_1 & 0 ¥¥
¥end{array}¥right]$](img369.png) |
|
|
(57) |
の掛け算になり,エピポーラ面に載る条件は,
 |
|
|
|
![$¥displaystyle =
{x_1}^T [{t_{12} ¥times}] ({¥rm R_{12}} {x_2} + {t_{12}}) =
{x_1}^T {¥rm E} {x_2} = 0$](img371.png) |
|
|
(58) |
となる.
この方程式は,┘團檗璽虔鏞璣epipolar equation) と呼ば
れる.行列
![${¥rm E}=[{t_{12} ¥times}]{¥rm R_{12}}$](img372.png) は靄楾堽
(E行列,essential matrix)と呼ぶ.デジタル画像座標系での座標
は靄楾堽
(E行列,essential matrix)と呼ぶ.デジタル画像座標系での座標
 と
と
 が与えられた時,
が与えられた時,
 ,
,
 より,
より,
 とおけば,
とおけば,
 |
|
|
(59) |
となる.この行列 は霑湛堽F行列, fundamental matrix)と呼ばれる.
2つのカメラ座標系の配置が決まれば,これらの基本行列または基礎行列が決まり,
エピポールの場所も一意に定まる.そして,注視点が与えられれば,その
投影点に対応するエピポーラ線も求めることができる.
は霑湛堽F行列, fundamental matrix)と呼ばれる.
2つのカメラ座標系の配置が決まれば,これらの基本行列または基礎行列が決まり,
エピポールの場所も一意に定まる.そして,注視点が与えられれば,その
投影点に対応するエピポーラ線も求めることができる.
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![¥includegraphics[width=7cm]{/home/inaba/text/iwanami/inaba/chap4/epipolargeometry.eps}](img357.png)
![$¥displaystyle [{x ¥times}] =
¥left[
¥begin{array}{ccc}
0 & -x_3 & x_2 ¥¥
x_3 & 0 & -x_1 ¥¥
-x_2 & x_1 & 0 ¥¥
¥end{array}¥right]$](img369.png)