

Next: 1.4 関節角の計算:逆運動学
Up: 1 ロボットアーム
Previous: 1.2 座標系の設定
関節角度列
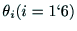 からハンドの位置と姿勢
からハンドの位置と姿勢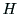 を計算する
ことは順運動学計算と呼ばれる.
図6において,ハンドに固定された座標系は,
を計算する
ことは順運動学計算と呼ばれる.
図6において,ハンドに固定された座標系は,
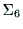 となる.
ハンドの位置は,基準座標系
となる.
ハンドの位置は,基準座標系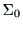 における
における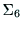 の
原点の座標で表される.
ハンドの姿勢は,座標系
の
原点の座標で表される.
ハンドの姿勢は,座標系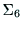 の
の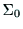 に対する回転変位によって表される.
6つの関節角
に対する回転変位によって表される.
6つの関節角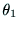 から
から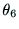 が与えられた時に,
ハンドの位置と姿勢を求める順運動学計算は行列
が与えられた時に,
ハンドの位置と姿勢を求める順運動学計算は行列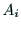 を用いて
簡単に表現できる.
座標系
を用いて
簡単に表現できる.
座標系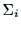 から
から
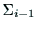 への座標変換は,
への座標変換は,
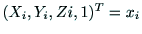 とおけば,
とおけば,
であり,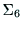 から
から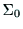 への座標変換は
への座標変換は
となる.ここで,
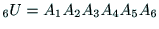 とおけば,
とおけば,
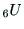 はハンド座標系
はハンド座標系
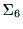 から基準座標系
から基準座標系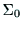 への座標変換を表す行列となる.
への座標変換を表す行列となる.
![$\displaystyle x_0 = {\rm _6U} x_6 =
\left[
\begin{array}{cccc}
& & & \\
& {\rm _6R} & & {\rm _6P} \\
& & & \\
& 0 & & 1 \\
\end{array}\right]
x_6$](img109.png) |
|
|
(2) |
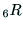 と
と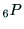 の要素は,
の要素は,
![$\displaystyle {\rm _6R}
=\left[
\begin{array}{ccc}
{\rm _6X} & {\rm _6Y} & {\rm...
... {\rm _6Z_y} \\
{\rm _6X_z} & {\rm _6Y_z} & {\rm _6Z_z} \\
\end{array}\right]$](img112.png) |
|
|
(3) |
![$\displaystyle {\rm _6P} =\left[
\begin{array}{c}
{\rm _6P_x} \\
{\rm _6P_y} \\
{\rm _6P_z}
\end{array}\right]$](img113.png) |
|
|
(4) |
3次行列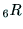 は,座標系の回転を表す行列であり,ハンドの姿勢を表
す.
は,座標系の回転を表す行列であり,ハンドの姿勢を表
す.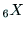 ,
, 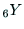 ,
, 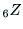 は,ハンドの座標系のX, Y, Z軸の
単位方向ベクトルであり,その要素は座標系
は,ハンドの座標系のX, Y, Z軸の
単位方向ベクトルであり,その要素は座標系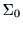 で表した方向余弦の値となる.
3次元ベクトル
で表した方向余弦の値となる.
3次元ベクトル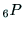 は,ハンド座標系
は,ハンド座標系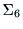 の原点の
の原点の
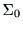 における位置を表し,ハンドの位置を表すことになる.
における位置を表し,ハンドの位置を表すことになる.
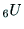 は,座標変換行列であるが,マニピュレータの基準座標系における
ハンドの位置と姿勢を表す一般形式となっている.
ハンドだけでなく,アームを構成する各リンクの位置と姿勢を求める場合も同
様である.リンク
は,座標変換行列であるが,マニピュレータの基準座標系における
ハンドの位置と姿勢を表す一般形式となっている.
ハンドだけでなく,アームを構成する各リンクの位置と姿勢を求める場合も同
様である.リンク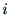 の位置と姿勢は,
の位置と姿勢は,
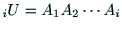 で表
すことができる.
マニピュレータの立体形状を描画で表示する場合には,各リンクの外形
代表点を基準座標系
で表
すことができる.
マニピュレータの立体形状を描画で表示する場合には,各リンクの外形
代表点を基準座標系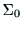 の座標として求めておく必要がある.
まず,リンク
の座標として求めておく必要がある.
まず,リンク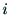 の外形を代表する点を
の外形を代表する点を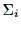 の座標
の座標
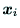 として
求めておく.関節角に対する
として
求めておく.関節角に対する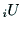 を求め,
を求め,
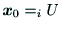
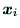 の座標変換を
行うことによって外形代表点の基準座標系
の座標変換を
行うことによって外形代表点の基準座標系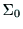 における座標が
求まる.
近年の三次元描画システムでは,表示するライブラリ側に各リンクを
表す立体形状の外形代表点をあらかじめ登録しておき,その立体の
位置と姿勢を変更するだけで自動的に座標計算を行って表示を行う
形になっている.その計算をハードウェアで行うことも可能で,高速な
三次元描画が可能となっている.三次元グラフィックス用のプロセッサ
はロボットに必要な座標変換計算と同様の計算機能を持っているものは
多く,汎用のプロセッサにおいても行列とベクトルの掛け算で必要
となる要素ごとの積をとり,その総和をとるといういわゆる積和
演算用の命令をもつものが増えてきている.
計算機言語が行列の計算表現を表す構文を持つ場合には,
その積和演算を呼び出すコンパイラを作ることができるが,
通常は,行列計算用のライブラリ関数を定義し,
そのライブラリ関数の内部でその拡張された命令を呼び出している
例が多い.
における座標が
求まる.
近年の三次元描画システムでは,表示するライブラリ側に各リンクを
表す立体形状の外形代表点をあらかじめ登録しておき,その立体の
位置と姿勢を変更するだけで自動的に座標計算を行って表示を行う
形になっている.その計算をハードウェアで行うことも可能で,高速な
三次元描画が可能となっている.三次元グラフィックス用のプロセッサ
はロボットに必要な座標変換計算と同様の計算機能を持っているものは
多く,汎用のプロセッサにおいても行列とベクトルの掛け算で必要
となる要素ごとの積をとり,その総和をとるといういわゆる積和
演算用の命令をもつものが増えてきている.
計算機言語が行列の計算表現を表す構文を持つ場合には,
その積和演算を呼び出すコンパイラを作ることができるが,
通常は,行列計算用のライブラリ関数を定義し,
そのライブラリ関数の内部でその拡張された命令を呼び出している
例が多い.
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
![\includegraphics[width=8cm]{/home/inaba/text/iwanami/inaba/chap4/sumitomo-coords.eps}](img87.png)
![$\displaystyle x_0 = {\rm _6U} x_6 =
\left[
\begin{array}{cccc}
& & & \\
& {\rm _6R} & & {\rm _6P} \\
& & & \\
& 0 & & 1 \\
\end{array}\right]
x_6$](img109.png)