

Next: 1.5 ヤコビ行列
Up: 1 ロボットアーム
Previous: 1.3 ハンドの位置と姿勢の計算:順運動学計算
ハンドの位置と姿勢を表す行列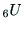 が与えられたとき,その位置と姿勢を実現するための6つの関節角を求めることを考える.この計算は逆運動学と呼ばれる.
が与えられたとき,その位置と姿勢を実現するための6つの関節角を求めることを考える.この計算は逆運動学と呼ばれる.
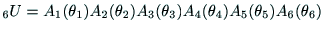 |
|
|
(5) |
を満足する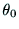 から
から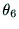 をこの方程式から直接求めることは
困難なので,アームの幾何学的構造を考慮に入れてジョイント角を求める.
ここで,アームの関節4,5,6の3軸が手首の点Wで交わる場合には,
W点の座標は
をこの方程式から直接求めることは
困難なので,アームの幾何学的構造を考慮に入れてジョイント角を求める.
ここで,アームの関節4,5,6の3軸が手首の点Wで交わる場合には,
W点の座標は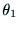 から
から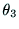 だけで決定される.
だけで決定される.
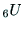 の値が与えられたとき,基準座標系
の値が与えられたとき,基準座標系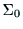 におけるW点の座標は次式により求められる.
におけるW点の座標は次式により求められる.
![$\displaystyle \left[
\begin{array}{c}
{\rm W_x} \\
{\rm W_y} \\
{\rm W_z} \\ ...
...array}\right]
\left[
\begin{array}{c}
0 \\
0 \\
-l_3 \\
0
\end{array}\right]$](img142.png) |
|
|
(6) |
図7に示すように,本アームでは,点S,点E,点Wは,
一つの平面上にある.
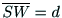 は,
は,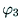 だけの関数であり,
関節3の可動範囲(
だけの関数であり,
関節3の可動範囲(
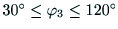 )を考慮に入れると,
)を考慮に入れると,
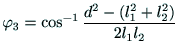 |
|
|
(7) |
| |
|
|
|
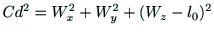 |
|
|
(8) |
である.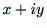 の偏角を
の偏角を 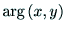 と表せば,
W点の座標と
と表せば,
W点の座標と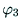 から
から
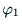 ,
,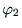 ,
,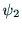 は次のように定まる.
は次のように定まる.
一般に,関節1,2,3の可動範囲に制限が無ければ,この解は4組存在しうる.
しかし,可動範囲がうまく選ばれていると解は1つになり,
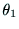 ,
,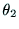 ,
,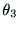 は次のように定まる.
は次のように定まる.
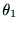 ,
,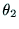 ,
,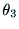 が定まれば,
が定まれば,
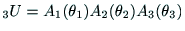 を計算することによ
り,座標系
を計算することによ
り,座標系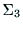 が設定されているリンク3の位置と姿勢がわかる.
が設定されているリンク3の位置と姿勢がわかる.
![$\displaystyle {\rm _3U}
=\left[
\begin{array}{cccc}
& & & \\
& {\rm _3R} & & {\rm _3P} \\
& & & \\
0 & 0 & 0 & 1 \\
\end{array}\right]$](img168.png) |
|
|
(15) |
![$\displaystyle =\left[
\begin{array}{cccc}
& & & \\
{\rm _3X} & {\rm _3Y} & {\rm _3Z} & {\rm _3P} \\
& & & \\
0 & 0 & 0 & 1
\end{array}\right]$](img169.png) |
|
|
|
ここで,
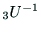 は,
は,
![$\displaystyle {\rm _3U^{-1}}
=\left[
\begin{array}{cccc}
& & & \\
& {\rm _3R^{-1}} & & -{\rm _3R^{-1}}{\rm _3P} \\
& & & \\
0 & 0 & 0 & 1
\end{array}\right]$](img171.png) |
|
|
(16) |
![$\displaystyle =\left[
\begin{array}{cccc}
& {\rm _3X^T} & & -{\rm _3X^T} {\rm _...
...{\rm _3Z^T} & & -{\rm _3Z^T} {\rm _3P} \\
0 & 0 & 0 & 1 \\
\end{array}\right]$](img172.png) |
|
|
|
である.
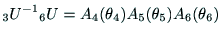 |
|
|
(17) |
である.
eq-u3-u6の回転部分に着目して成分を比較すると,
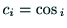 ,
,
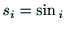 と表すとして,
と表すとして,
となり,
となる.ここで,
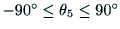 であれば,
であれば,
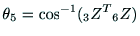 |
|
|
(23) |
となるが,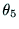 には正負つの解があり,それに対応して,
には正負つの解があり,それに対応して,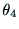 ,
,
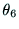 は以下の二通りの解がある.
は以下の二通りの解がある.
- (1)
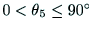 のとき
のとき
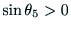 より
より
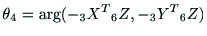 |
|
|
(24) |
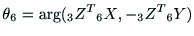 |
|
|
(25) |
- (2)
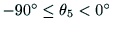 のとき
のとき
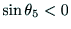 より
より
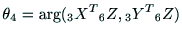 |
|
|
(26) |
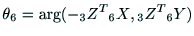 |
|
|
(27) |
もし,
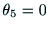 のときには,
のときには,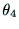 ,
,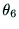 は不定である.
また,図6の幾何学的な構造から,座標系
は不定である.
また,図6の幾何学的な構造から,座標系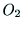 ,
,
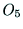 の座標軸の関係から求めることもできる.
の座標軸の関係から求めることもできる.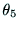 は,
は,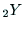 と
と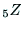 のなす角であり,
のなす角であり,
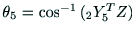 となる.
となる.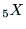 と
と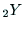 の為す角が
の為す角が
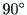 以内であれば,
以内であれば,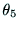 は正
であり,
は正
であり,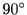 以上であれば,負である.
以上であれば,負である.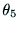 が正であれば,
が正であれば,
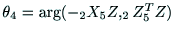 ,
,
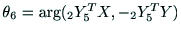 となり,そうでなければ,
となり,そうでなければ,
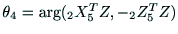 ,
,
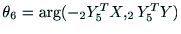 とな
る.
とな
る.


Next: 1.5 ヤコビ行列
Up: 1 ロボットアーム
Previous: 1.3 ハンドの位置と姿勢の計算:順運動学計算
generated through LaTeX2HTML. M.Inaba 平成18年5月7日
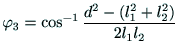
![$\displaystyle =\left[
\begin{array}{ccc}
{\rm c_4c_5c_6 - s_4s_6} & {\rm -c_4c_...
...s_4c_5s_6 - s_4c_6} & -s_4s_5 \\
s_5c_6 & -s_5s_6 & c_5 \\
\end{array}\right]$](img177.png)